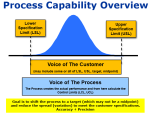
Probability Density Function 

The Probability Density Function (PDF) is referred to as the shape of the distribution. PDF is used to define the probability of a random variable occurring within a range of values. 

As a histogram of the distribution is created with more and more categories, it begins to take on the exact shape of the distribution.

If you were to draw a curved line that fits most of the histogram (created from the samples) it would create a model that describes the population. 

• X-axis: represents the z-scores of measurement
• Y-axis: represents, within +/- 0.5 standard deviation, the probability of "x" occurring with each "x" being independent

We will call f(x) the PDF which is the curved line overlaid on the samples of the histogram. The area to the left of x (point of interest) is equal to probability of the x-axis variable being less than the value of x (point of interest). The probability density is the y-axis.

The PDF works for discrete and continuous data distributions. There PDF must be positive for all values of x since there can not be a negative value for probability. 

The PDF represents the entire amount of space under the curve and the highest probability that exist is 100% or 1.00 the entire area under the curve = 1.

So, from negative infinity to positive infinity, the area under the curved line is represented by the following integral:

ShareFacebookXWhatsApp

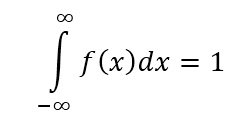
The PDF for discrete data for all values of k with f(x) greater than or equal to 0:

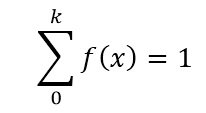
The integral of the PDF to the left of a point of interest, "x", is the Cumulative Distribution Function (cdf). 

Normal PDF in Excel

The function NORM.DIST (former Excel version used NORMDIST) calculates the Normal Probability Density Function or the Cumulative Normal Distribution Function. 

The Normal PDF is defined by two values:

1. Mean
2. Standard Deviation

and creates a bell-shaped probability density function. 

The mean is the measurement of central tendency and the standard deviation is the spread (or dispersion) of the distribution around the mean. 

With "x" as the point of interest, the format of the function is:

NORMDIST(x, mean, standard deviation, TRUE or FALSE)

In the final argument use TRUE for the Cumulative Normal Distribution Function and use FALSE for the Normal Probability Density Function.

What is the CDF and inverse CDF?

Click here to learn about the Cumulative Density Function and its inverse. 

Return to BASIC STATISTICS

Return to the MEASURE phase

Six Sigma Templates, Statistics Tables, and Calculators

Search Six Sigma related job openings