Six Sigma Financial Savings

It's easy to get caught up in the weeds of statistics and tools but remember the ultimate goal of Six Sigma is to make money and increase profits.

The projected financial savings must be analyzed by the Project Manager in conjunction and validation from a Controller or a financial representative.

A project does not have to contribute to ROI or directly increase revenue to qualify as a Six Sigma project. Many forms of soft savings related projects include customer scorecard improvements, loyalty, satisfaction, risk avoidance, and cost avoidance. The reduction of risk, while hard to measure, can increase profit.

Some of the guidelines below may fall under both categories of hard and soft savings in different percentages. Each company may categorize them slightly different. It is important to understand and adhere to your company reporting guidelines.

Before a project begins, a preliminary estimate of the hard and soft savings must be determined and agreed upon by the BB/GB, financial representative, and the MBB or representative of Upper Management.

The GB/BB should possess a firm understanding of financial relationships, variances, and projected impact of their project. The reported savings may be audited therefore tracking accuracy is critical. It is equally important to analyze the financial savings and costs by financial reporting period.

Why is the removal of "waste" important?

The primary objective in the removal of waste (Lean Manufacturing) is to reduce the amount of time in the Order Production Cycle where starts at the time from of receipt of an order (often in the legal form of a Purchase Order) to the time of receipt of payment. In other words, reduce or compress the cash conversion cycle.

The goal is to get paid for an order a close to the time as you have to spend money to make that product or service. In some cases, you may be able to get prepaid.

The quicker payments are received, the lower the cost of borrowing for the company and gives the company an opportunity to invest or otherwise apply that money. This can lead to further hard and/or soft savings.

Some examples of savings are shown below but each company likely has it's own definitions, policies, and procedures for handing financial reporting.

HARD Savings

Hard savings means there is a direct flow to the Profit and Loss statement (P&L).

Moving from one operation to less expensive operation.
Permanently remove labor, wages, benefits, etc.
Sell a building, or end lease/rent real estate.
Eliminate direct material costs or reduce to lower cost level.
Reduction in insurance premiums.
Reduce indirect materials cost or eliminate the use.
Reduced inventory levels of product or material, or reduce cost of carrying the same level, often at the WACC.
Sold equipment directly related to project efforts (must exceed Net Book Value in some cases to be counted as savings. Some will consider these sunk costs so any sale is savings).
Overtime reduction.
Eliminated sorting by instituting poka-yoke to prevent defects.
Utility or natural resource reduction or elimination.
Scrap dollars reduced or eliminated.
New product revenue.
Eliminate storage fees.
Reduction annual maintenance fees from one year to the next.
Eliminate off-site storage fees after a 5S event.
Reworking obsolete raw material or tooling.
Getting higher amount of credit for recycling efforts such as selling used oil, using "used" packaging, "used" pallets, or scrap metal.
Selling back spare parts that have already been expensed (sunk costs). The P&L impact is the sale price minus the remaining net book value so be careful it could result in a P&L loss.
Taking advantage of a payment term discount when the savings exceeds your company's weighted average cost of capital (WACC) or also known as the hurdle rate. However, this impacts cash flow and working capital so this should be negotiated with approval of Finance.

SOFT Savings

Soft Savings do not have a direct impact on the P&L.

Intangible savings.
Improving 5S score of an area.
Reduce RPN on PFMEA for particular failure mode Improved customer/employee satisfaction.
Reduced insurance levels due to reduced hazards, exposure, or frequency. (This could be hard savings if cost of insurance is reduced too).
Shift work task of employees but overall hours worked are not reduced.
Improve service level (unless it can be documented that it directly related to new sales or profit).
Improved ergonomics or environmental, health, and safety conformance (may be hard savings if it directly avoids a fine that has been accrued for).
Reduced walking distance of an operator.
Alleviated floor space or machinery but it is not sold or used to produce new income.
Avoiding the purchase of additional planned equipment or material.
Future manpower need reductions.
Improves morale of workforce or customers.
Reduce projected warranty costs.
Adding a longer warranty.
Working with supplier to hold spare parts for JIT delivery.
Adding a discount payment term option in addition to the existing fallback payment option. Such as adding a 2% N15 to standard N45 terms. If your company takes advantage of this discount it will be a hard savings as indicated above. However, it will negatively impact cash flow and depending on your companies WACC this may or may not be a good option.

Working Capital (CASH FLOW)

Some projects may have a problem statement that involves improving working capital or cash flow. Almost every Six Sigma project has some impact on working capital.

Some areas to be aware of the could help your project deliver a bigger reward is to improve these areas that impact working capital.

Extension of payment terms
Delaying payment of purchases, such as going to expensing upon receipt to consignment (expensing upon use)
Improving time to get receivables
Reducing your company's WACC through interest rate reductions, etc.

EXAMPLE:

One calculation to determine the impact from a change in payment terms is shown below:

Annual Spend / 365 * # of days increased (or shortened).

If Supplier A was at N45 (net 45 days) and the annual spend is $15,000,000 and your team negotiates N60 terms then the calculation is as follows:

$15,000,000 / 365 * +15 days = $616,438 annually

An additional $616,438 of cash (working capital) is available to put towards debt or fund other investments that wasn't before.

If that money is put towards paying down debt, then the hard savings may be estimated by taking the savings * your company's WACC.

Assume the WACC is 10% for your company then the hard savings can be estimated at $61,438.

The is a simplistic estimate. Each company will have specific guidelines and exceptions. This information is intended to spawn ideas for your team to deliver more results.

Keep in mind sometimes payment terms may be negotiated lower thus negatively impacting cash flow in favor of a piece price reduction that is more than overall favorable.

Typical Financial Reporting Rules

Six Sigma financial reporting is necessary to show the impact on the P&L of a respective business unit, facility, and entire company.

Each company will need to define the rules and guidelines for accountability, accuracy, and consistency.

The plan should include:

Standard definitions and rules
Roles and responsibilities for all parties involved
Hard savings versus Soft savings
Understand of working capital impacts
Quick method to report savings, validate, and upload (if necessary)
Costs to be included in overall project impact
Reporting times and reporting calendar
Exchange rate rules
Clarify conflicts in savings
Understand what levers are most important in negotiations

Often times many departments are accountable for generating savings and Six Sigma is certainly one of them (others may be Supply Chain and Human Resources).

Since teams are meant to be cross functional, there will be instances where teams have members of two or more of these departments and all are looking to report savings. There should be a policy with examples to guide the savings distribution process.

There should be a database with all projects and their status relative to their FINANCIAL contribution: For example, a project may be closed but the company allows savings to be reported for 12 months since the first month of savings.

If the savings grow over time then and uniform distribution of the full savings rate per month * 12 should be given credit.

Cost Accounting vs Throughput Accounting

Cost Accounting places a strong emphasis on reducing costs, (aka cutting expenses) and this is often leads to decisions that reduce headcount, trimming of employee benefits and a myriad of squeezes that are not the goal of Six Sigma or Lean Manufacturing and actually give these programs a bad reputation.

Lean Manufacturing focuses on the Theory of Constraints, or removing bottlenecks to increase throughput and thus increases Sales (revenue) or make available capacity to take on more sales and growth. Then the company can devote that cost-cutting energy and devote it to growing the "top line" which is sales.

Cutting expenses is limited at some point. A company can only trim so much and often they cross a tipping point where the risk and losses long term exceed any short-term gain. The most damaging correlation a company can be perceived to have is one where improvements from Lean Manufacturing or Six Sigma programs results in headcount reduction (or even overtime reduction).

If the employees, or stakeholders, perceive that these programs reduce their personal or family quality of life in any way, then the program is not likely to succeed...very simple.

The top line growth is seen as being unlimited and is where the competitive advantages can reside. Therefore, the most commonly ask question by company leaders is how to grow the top line which includes increasing throughput with minimal investment or increase in operating expenses.

Three key words:

Throughput
Operating Expenses
Investment

In Throughput Accounting, there are a few basic formulas used:

Net Profit = Throughput − Operating Expenses

Productivity = Throughput / Operating Expenses

Investment Turns = Throughput / Investment

Return on Investment = Net Profit / Investment

You can see how they are all tied together which an emphasis that increases in throughput drive the most potential for the company.

Finance responsibilities

Quantify the savings being generated by the project.
Determine how to handle Balance Sheet reductions, typically not hard savings.
Determine if savings are hard savings or soft savings.
Ensure that the realization of the savings can be tracked.
Ensure that the CFO (or Upper Management) agrees with the figures.
Ensure that the reported savings can be audited.
Ensure the hard savings are reflected in future budgets.

Future Value of money (FV)

Calculating FV is an important concept to project a future amount based on inputs of expected interest rate, number of time periods, beginning amount, and payments for the period. (assumed constant over each period).

FV is the value of a current asset (or amount of money) at some point in the future based on an assumed growth rate. There are two commonly used formulas:

1) The basic formula for simple interest (not compounding) is

FV = I * (1 + (R * T))

where

I = initial investment amount (or current asset value) or present value
R = annual interest rate
T = number of years

The time interval could be 'months' or any time interval as long as they are the same units for R and T.

Example:

What is the FV of a $10,000 investment after 8 years that earns 5% simple interest annually?

FV = 10,000 * (1 + (0.05 * 8))

FV = 10,000 * (1 + 0.4)

FV = 10,000 * 1.4 = $14,000

2) The basic formula for compounding interest is shown below:

FV = I * (1 + R)^T

where

I = initial investment amount (or current asset value) or present value
r = annual interest rate
n = number of periods interest is held

Example:

Using the same example for 1) but using compounding interest. What is the FV of a $10,000 investment after 8 years that earns 5% compounding interest annually?

FV = 10,000 * (1 + 0.05)⁸

FV = 10,000 * (1.05)⁸

FV = 10,000 * 1.477 = $14,770

The final result between 1) and 2) is an increase of $770 over eight years as a result of compounding interest (i.e. earning interest on the interest earned from the previous time period) each year instead of solely simple interest.

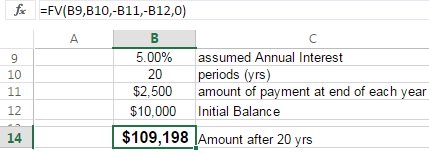
More advanced example

The following is more complex example done in Excel with the following assumptions:

5% annual interest rate
Plan to make 20 payments at end of each year for 20 years.
Using Excel means that a '0' is used for this input.
The amount of the payment added at the end of each year is $2,500
The amount at the beginning is $10,000 (present value)

The answer is $109,198. The ability to run scenarios with money that is freed up from a project is useful to help make investment decisions.

This obviously has a very practical use in personal lives as well. The above example is similar to a savings plan for a child's college tuition.

The picture below shows the basic formula and how to enter into Excel.

If you want to find I (or the Present Value PV), simply rearrange the formula above:

Present Value (I) = FV / (1+r)ⁿ

Return on Investment (ROI)

ROI is possibly the most commonly used calculation to determine payback but there are several more and variations. We'll keep it simple here. There will likely be questions on a Six Sigma certification exam (especially for Black Belts) about some key financial metrics

One version of calculating ROI is:

ROI = Net Investment / Investment Cost * 100%

Another is:

ROI = Net Profit (Income) / Investment Cost * 100%

where the net profit (income) is expected earnings

Another is:

ROI = (FVI - IVI) / Investment Cost * 100%

FVI = Final value of Investment

IVI = Initial value (or cost) of Investment

At a high level, think of it as the

(AMOUNT GAINED - AMOUNT SPENT) / (AMOUNT SPENT) * 100%

Return on Assets (ROA)

ROA = Net Income / Total Assets * 100%

where the net income is the expected earnings from the total value of the assets applicable on the project.

Example:

Assume Company A has net income of $50,000 and Company B has net income of $45,000 over the same period of time. Company A has total assets of $1,000,000 and Company B has only ¾ of the Company A assets. Which Company has a higher ROA?

Company A ROA = $50,000/$1,000,000 = 5%

Company B ROA = $45,000/$750,000 = 6%

Net Present Value (NPV)

Calculating the NPV of each project is one method used to evaluate projects ability to deliver to the company's financial expectations. Like any metric, the results needs to be faced with reality. Sometimes are project may be high risk and the potential return can't be justified.

We won't get into the details around the formula shown below since it can be complicated and done in various ways. Leave this up to the Finance representative for the team.

You should know that a POSITIVE NPV is generally worth approving for a given cost of capital.

This is different than IRR where the NPV is set to a value of zero and the internal rate of return, r, (IRR) is calculated and compared to other projects.

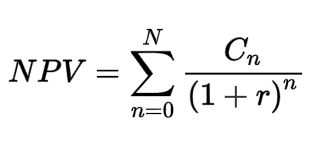
Internal Rate of Return (IRR)

The IRR is calculated to determine an investment's internal rate of return which is denoted by r in the formula above. The word 'internal' infers that the calculation does not include external factors such as the WACC, financial risk, or inflation.

The value, r, which represents the internal rate of return, (aka interest rate or discount rate) is solved for in the formula below when the NPV is set to a value of 0.

IRR values for several projects of often compared to each other by a company. Those with the higher IRR are expected to have the best financial benefit.

The basic equation is above however we won't cover an example, just understand these basic concepts of NPV and IRR.

Projects that have a 10% IRR may be sufficient for one company but not another. Each company has it's own acceptability criteria but higher IRR the better the return.

Projects that have an IRR that is higher than the company's ROI are to be prioritized since they can boost the company's overall ROI after the project is implemented.

Calculating Payback Period

The Payback Period (PP) represents the amount of time for the project to pay off the initial and incremental investments.

The formula can be quite complex if considering the time value of money, taxes, interest, and cash inflows or further expenses beyond the payback period.

For the sake of keeping it simple, we will ignore those factors in the example below and this example should represent what you might encounter on a certification exam.

FORMULA:

PP = (Initial + Incremental Invested Amount) / Cash Inflow

The Cash Inflow is typically expressed in $ that the project is expected to save per YEAR or per MONTH.

EXAMPLE:

Calculate the PP for a project that requires a $50,000 investment up front plus $10,000 per month for the first 5 months. The projected savings are $12,000 per month starting in the sixth month after the initial investment.

PP = (($50,000 + ($10,000 * 5)) / ($12,000)) + 5 months*

PP = ($100,000 / $12,000) + 5 months

PP = 8.33 months + 5 months = 13.33 months

Therefore, the first positive full month will be the 14th; the PP = 14 months

*5 months is added since the savings start at the 6th month.

Project Contract template

Return to the DEFINE phase

Learn about Economic Order Quantity

Search for Six Sigma job openings

Return to the home page