Box-Cox Transformation

The Box-Cox Transformation is one method of transforming non-normal data, or data that cannot be assumed normal, to meet a normal distribution and allow further capability analysis and hypothesis testing.

The term is named after statisticians George and David Cox which is a method that uses an exponent, Lambda, to transform the data.

The value of Lambda is the power to which each data point is raised X^l

Then a new (transformed) set of data is created and that transformed set of data is used in for statistical analysis.

The tool is typically used in the ANALYZE phase of a DMAIC project.

Data Assumptions for using Box-Cox:

Continuous X and Y
Data does not contain negative numbers or zero
The order of data must remain the same after the transform is complete
Data being transformed must be smooth and continuous (multimodal or bimodal data can not be transformed using this technique)
Maximum observation in original data must be at least twice as large as the minimum such as 5 to 10.
The specifications (such as LSL and USL) must also be transformed if a capability analysis is being performed and be >0.

When the data is not normally distributed, this could result in inaccuracies when calculating a z-score. This could result in an inaccurate representation of your process capability.

Control charts may depict a process that is more or less in control than in reality; and, when performing a hypothesis tests the results of your tests may not be accurate, especially as the data is less normal.

NOTE

A Box-Cox transformation for ln (l = 0) requires that the LSL, USL and data are >0. You may find that your lower specification limit (LSL) is originally < or = 0. If your LSL is zero, this requires a offset to each the LSL, the data, and USL.

Often the LSL may not be specified but it is known to be a Lower Bound (LB). Such as if you are evaluating pieces per hour and Parts Per Million (PPM). It is not possible to have <0 but a LB of exactly 0 does exist.

For example:

If you have a LSL of 0.0 and an USL of 5.0, you can add 0.1 to the LSL to make it 0.1 and the USL becomes 5.1. You must also add 0.1 to all the original data points.

Then run the Box-Cox transformation (after you verify the transformed data is normal, should get a p-value > 0 on the transformed data) and get your PPM.

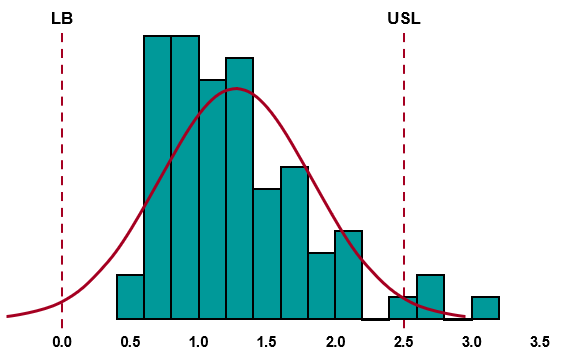
The data analyzed below has a P-value of 0 and thus is non-normal. You can the see the LSL (or LB) is = 0. When running a Box-Cox transformation for ln (l = 0), add an offset such as 0.01 or 0.1 to all the data points, LB, and USL and run the transformation.

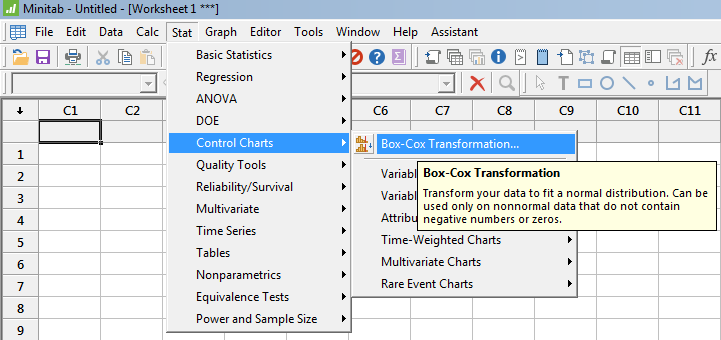
Box-Cox Transformation using Minitab

The menus may change depending on the version of Minitab being used. However, the concept and general flow of the process will be similar. Use the 'Help' menu to advise on how to conduct this transformation using your version.

Return to Basic Statistics

Return to the ANALYZE Phase

Templates and Calculators

Test your Six Sigma knowledge with these practice problems