Subscribe To This Site
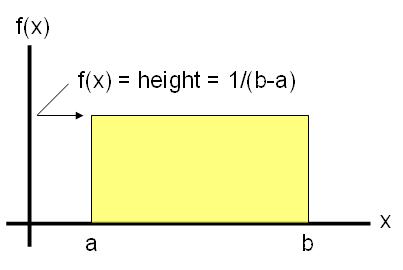
Uniform DistributionAlso known as a rectangular distribution. The uniform distribution lies between two values on the x-axis. The total area is equal to 1.0 or 100% within the rectangle. Most statistical software programs have capability to solve for probabilities for the uniform distribution.
Example
Return to BASIC STATISTICS Shop at the Six-Sigma-Material store Search active job openings related to Six Sigma Return to the Six-Sigma-Material Home Page from Uniform Distribution
|
