P-value

The p-value (probability value) represents the probability that the change is due to random, inherent sources. It's used to measure the significance of sample (observed) data. A p-value calculation helps determine if the observed relationship could arise as a result of chance.

It is one of the quantitative values used to make a decision regarding the validity of the null hypothesis based on the testing results.

The lower the p-value, the lower the risk of being wrong when the decision is made to reject the null and infer the alternative hypothesis (and vice versa).

P-Value at Six-Sigma-Material.com

Most often there are three test statistics used in hypothesis testing:

Z-test statistic

t-test statistic

F-test statistic

P-values are found in in t-tests, z-tests, distribution tests, ANOVA (uses F-test), and regression testing.

In a Six Sigma project, a Black Belt may uses hypothesis testing to test an effect of some sort, such as the effect related to an operator, material, machine, improvements, or any number of things.

The Black Belt is looking to detect a difference or change and to quantify the change. After the IMPROVE phase, most likely looking to prove a positive change in performance.

A p-value of 0.005 indicates that if the null hypothesis tested were indeed true, then there would be a 5-in-1,000 chance of observing results at least as extreme. This leads the observer to reject the null hypothesis, H_O because either a highly rare data result has been observed or the null hypothesis is incorrect. Therefore the H_A is inferred.

ShareFacebook X WhatsApp

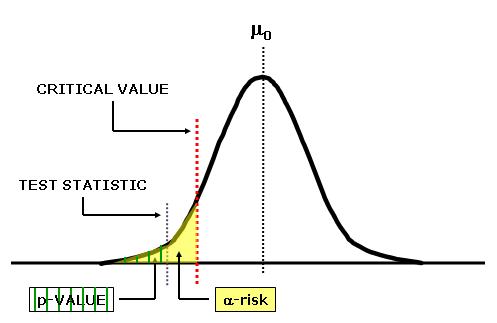
The TEST STATISTIC is calculated (aka T_calc) and could be located anywhere in the picture above.

The calculated test statistic (depending on which comparison test is being used) is compared to the critical statistic of that same distribution (such as Z, t, F) to decided whether to "reject" or "fail to reject" the null hypothesis.

The formulas for each test statistics are shown in the hypothesis testing section where there is more information on using the p-value in statistical tests.

IF the...

calculated test statistic is > than the critical statistic (found from a table),

THEN the...

decision is to reject the null hypothesis.

Using this method requires a calculation on the degrees of freedom, which requires only knowing the sample size(s).

Another method of making a decision in a hypothesis test is by comparing the calculated p-value to the alpha risk .

If the p-value is > Alpha Risk, fail to reject the Ho (null hypothesis)
If the p-value is < Alpha Risk, reject the Ho (null hypothesis) and the data can be assumed normal.

Recall: Level of Confidence = 1 - alpha risk

Higher and higher p-values means the results from the sample are more and more consistent with the null hypothesis, H_O and vice versa. The lower the p-value the stronger the case is against the null hypothesis. A p-value of 0.03 and 0.008 may both be below the alpha risk of 0.05 but 0.008 has the stronger case and evidence against the H_O,

Assessing Normality

The p-value is also used to determine if a data distribution meets the normality assumptions. Generally, with an alpha risk of 0.05 this would mean the Confidence Level = 0.95 or 95%.

If the p-value is greater than 0.05 then the data is assumed to meet normality assumptions. There is a single point of central positioning (mean ~ median ~ mode) and bell-shaped distribution within the histogram. In the ANALYZE phase, Six Sigma project managers would apply parametric tests.

The data can still be assumed normal if there can be outliers when generating a Box Plot. Outliers do not automatically indicate a non-normal distribution.

Equal (or unequal) Variances?

Most statistical software programs have an option to select 'Equal Variances' when running a t-test or ANOVA. The assumption of unequal variances impacts the overall estimate of the variance related to error. This impacts that z, t, and f statistics values.

The p-value in reality is higher than the calculated p-value when the assumption of equal variances is violated. In other words, the probability of making a Type I error is actually larger than calculated.

If you are assuming equal variances, then this assumption should be tested (similar to testing the residuals in a Regression or ANOVA test for normality to meet their respective assumption).

Caution

P-value calculations in spreadsheets such as Excel can be tricky. Even when using statistical software you need to ensure the correct options are selected.

Possible sources of error are:
Flaw in data (as with any test or calculation, mistakes in the data entry are a problem)
Incorrect formula selection
Misinterpretation of the calculated p-value
Incorrect assumptions such as normality, equal variances, etc.
Wrong use of one-tail or two-tailed tests
Outliers are special causes in data

Why P = 0.05?

Click here to read an excellent description on the reasoning why 0.05 was selected as the general criteria to determine statistical significance. A p-value of 0.05 or lower is generally considered statistically significant but may not be suitable for every case.

In Summary

The p-value is used to measure the significance of observational data which are samples. When an apparent relationship between two variables of the sampled data, there remains the possibility that this correlation might be a coincidence.

A p-value calculation helps determine if the observed relationship could arise as a result of chance.

The p-value tells you whether or not the null hypothesis (H_O) is supported; it does not tell you if the alternative hypothesis (H_A) is true or false.

When your results are on the fence, try to get more samples. Samples increase the power and strengthen the decision making process.

Return to the ANALYZE phase

Return to BASIC STATISTICS

Templates, Tables, Calculators

Six Sigma related job openings

Return to Six-Sigma-Material Home Page