P-Chart

Attribute (Discrete) Control Charts

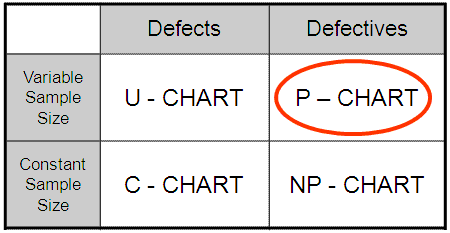
A P-Chart is an attribute control chart used when plotting:

1. DEFECTIVES
2. BINOMIAL ASSUMPTIONS SATISFIED
3. VARIABLE SAMPLE (SUBGROUP) SIZE (will also plot constant sample size)

Each observation is independent. The word "defective" is also sometime referred to as "nonconforming". The P-Chart is also referred to as a control chart for fraction nonconforming. 

The purpose is to develop upper and lower control limits (UCL and LCL) and determine performance of process over time. This chart plots the proportion (fraction, percent) of defective units in a constant or variable size sample.

This is the most sensitive and commonly used attribute control chart. 

The variable sample size should each be of a size to have the likelihood that it contains at least one defect. If the defective level is very low, (sample size * average % defective < 5), then apply binomial distribution exact limits. The chart should not be applied if one defect puts the process out of control.

The chart is normally used to detect shifts >1.5 standard deviations. In order to detect smaller and quicker shifts there are other charts for variable and attribute data such as Exponentially Weighted Moving Average (EWMA) and Cumulative Sum of Quality Characteristic Measurement (CUSUM). These are referred to as time-weighted moving charts.

The P-chart is displayed as a fraction (or % or proportion).

• The C chart displays the number of defects
• The U chart displays the number of defects per unit
• The NP chart displays the number of defectives

For P charts, the subgroup size may vary but they should each be >50.

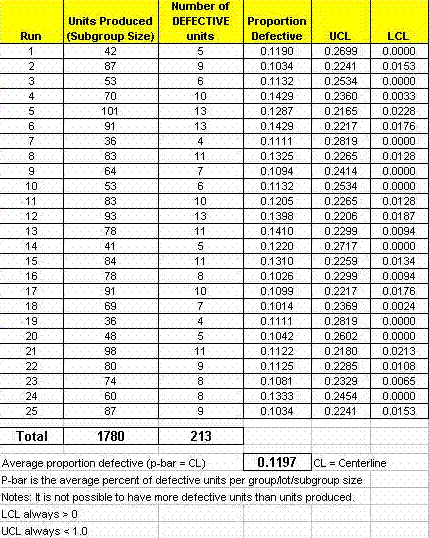
Below is a sample set of data which will help illustrate the creation of the P-chart, its centerline and control limits.

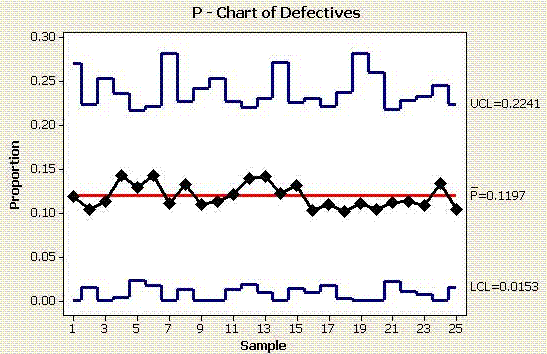
From the data set above the following graph is produced. Many statistical programs offer a variety of options for establishing the limits and centerline descriptions.

The average proportion of defective units (not defects) is 11.97%. Based on the control limits, the process "voice" is telling us that it is expected that between 1.53% and 22.41% of the units will be defective each run. 

Review of other attribute control charts:

NP - Chart

U - Chart

C - Chart

---

Return to SPC Charts

Return to the MEASURE phase

Return to the CONTROL phase

Return to the Six-Sigma-Material Home Page